Rotary Position Embeddings for Long Context Length

Source: MachineLearningMastery.com

Rotary Position Embeddings (RoPE) is a technique for encoding token positions in a sequence. It is widely used in many models and works well for standard context lengths. However, it requires adaptation for longer contexts. In this article, you will learn how RoPE is adapted for long context length.

Let’s get started.

Rotary Position Embeddings for Long Context Length
Photo by Nastya Dulhiier. Some rights reserved.

Overview

This article is divided into two parts; they are:

Simple RoPE
RoPE for Long Context Length

Simple RoPE

Compared to the sinusoidal position embeddings in the original Transformer paper, RoPE mutates the input tensor using a rotation matrix:

$$
begin{aligned}
X_{n,i} &= X_{n,i} cos(ntheta_i) – X_{n,frac{d}{2}+i} sin(ntheta_i) \
X_{n,frac{d}{2}+i} &= X_{n,i} sin(ntheta_i) + X_{n,frac{d}{2}+i} cos(ntheta_i)
end{aligned}
$$

where $X_{n,i}$ is the $i$-th element of the vector at the $n$-th position of the sequence of tensor $X$. The length of each vector (also known as the hidden size or the model dimension) is $d$. The quantity $theta_i$ is the frequency of the $i$-th element of the vector. It is computed as:

$$
theta_i = frac{1}{N^{2i/d}}
$$

A simple implementation of RoPE looks like this:

import torch

import torch.nn as nn

def rotate_half(x: torch.Tensor) -> torch.Tensor:

“”“Rotates half the hidden dims of the input.

This is a helper function for rotary position embeddings (RoPE).

For a tensor of shape (…, d), it returns a tensor where the last

d/2 dimensions are rotated by swapping and negating.

Args:

x: Input tensor of shape (…, d)

Returns:

Tensor of same shape with rotated last dimension

““”

x1, x2 = x.chunk(2, dim=–1)

return torch.cat((–x2, x1), dim=–1) # Concatenate with rotation

class RotaryPositionEncoding(nn.Module):

“”“Rotary position encoding.”“”

def __init__(self, dim: int, max_position_embeddings: int) -> None:

“”“Initialize the RotaryPositionEncoding module

Args:

dim: The hidden dimension of the input tensor to which RoPE is applied

max_position_embeddings: The maximum sequence length of the input tensor

““”

super().__init__()

self.dim = dim

self.max_position_embeddings = max_position_embeddings

# compute a matrix of ntheta_i

N = 10_000.0

inv_freq = 1.0 / (N ** (torch.arange(0, dim, 2).float() / dim))

inv_freq = torch.cat((inv_freq, inv_freq), dim=–1)

position = torch.arange(max_position_embeddings).float()

sinusoid_inp = torch.outer(position, inv_freq)

# save cosine and sine matrices as buffers

self.register_buffer(“cos”, sinusoid_inp.cos())

self.register_buffer(“sin”, sinusoid_inp.sin())

def forward(self, x: torch.Tensor) -> torch.Tensor:

“”“Apply RoPE to tensor x

Args:

x: Input tensor of shape (batch_size, seq_length, num_heads, head_dim)

Returns:

Output tensor of shape (batch_size, seq_length, num_heads, head_dim)

““”

batch_size, seq_len, num_heads, head_dim = x.shape

dtype = x.dtype

# transform the cosine and sine matrices to 4D tensor and the same dtype as x

cos = self.cos.to(dtype)[:seq_len].view(1, seq_len, 1, –1)

sin = self.sin.to(dtype)[:seq_len].view(1, seq_len, 1, –1)

# apply RoPE to x

output = (x * cos) + (rotate_half(x) * sin)

return output

The code above defines a tensor inv_freq as the inverse frequency of the RoPE, corresponding to the frequency term $theta_i$ in the formula. It is called inverse frequency in the RoPE literature because it is inversely proportional to the wavelength (i.e., the maximum distance) that RoPE can capture.

When you multiply two vectors from positions $p$ and $q$, as you would do in the scaled-dot product attention, you find that the result depends on the relative position $p – q$ due to the trigonometric identities:

$$
begin{aligned}
cos(a – b) = cos(a) cos(b) + sin(a) sin(b) \
sin(a – b) = sin(a) cos(b) – cos(a) sin(b)
end{aligned}
$$

In language models, relative position typically matters more than absolute position. Therefore, RoPE is often a better choice than the original sinusoidal position embeddings.

RoPE for Long Context Length

The functions $sin kx$ and $cos kx$ are periodic with period $2pi/k$. In RoPE, the term $theta_i$ is called the frequency term because it determines the periodicity. In a language model, the high-frequency terms are important because they help understand nearby words in a sentence. The low-frequency terms, however, are useful for understanding context that spans across multiple sentences.

Therefore, when you design a model with a long context length, you want it to perform well for short sentences since they are more common, but you also want it to handle long contexts that your model should support. You do not want RoPE to treat every sequence length equally.

The strategy is to reallocate the RoPE scaling budget: apply a scaling factor to improve long-range stability (at low frequencies of sine and cosine) while avoiding scaling when local position information is important (at high frequencies of sine and cosine).

In Llama versions 1 and 2, RoPE is implemented with a maximum length of 4096, similar to the previous section. In Llama 3.1, the model’s context length is expanded to 131K tokens, but RoPE is calculated using a base length of 8192. The implementation is as follows:

import torch

import torch.nn as nn

import math

def rotate_half(x: Tensor) -> Tensor:

“”“Rotates half the hidden dims of the input.

This is a helper function for rotary position embeddings (RoPE).

For a tensor of shape (…, d), it returns a tensor where the last

d/2 dimensions are rotated by swapping and negating.

Args:

x: Input tensor of shape (…, d)

Returns:

Tensor of same shape with rotated last dimension

““”

x1, x2 = x.chunk(2, dim=–1)

return torch.cat((–x2, x1), dim=–1) # Concatenate with rotation

class RotaryPositionEncoding(nn.Module):

“”“Rotary position encoding.”“”

def __init__(self, dim: int, max_position_embeddings: int, base_length: int = 8192) -> None:

“”“Initialize the RotaryPositionEncoding module

Args:

dim: The hidden dimension of the input tensor to which RoPE is applied

max_position_embeddings: The maximum sequence length of the input tensor

base_length: The base length of the RoPE

““”

super().__init__()

self.dim = dim

self.max_position_embeddings = max_position_embeddings

# compute a matrix of ntheta_i

N = 10_000.0

scale_factor = 8.0

low_factor, high_factor = 1.0, 4.0

base_length = 8192

# Compute the inverse frequency based on the standard RoPE formula

inv_freq = 1.0 / (N ** (torch.arange(0, dim, 2).float().to(“cuda”) / dim))

# Compute the modified inverse frequency

# scaled if freq too low, orig if freq too high, smoothed if in between

wavelen = 2 * math.pi / inv_freq

max_wavelen = base_length / low_factor

min_wavelen = base_length / high_factor

smooth_factor = (base_length / wavelen – low_factor) / (high_factor – low_factor)

smoothed = (1 – smooth_factor) * inv_freq / scale_factor + smooth_factor * inv_freq

inv_freq = torch.where(wavelen > max_wavelen, inv_freq / scale_factor,

torch.where(wavelen < min_wavelen, inv_freq,

smoothed))

# multiply with sequence length

inv_freq = torch.cat((inv_freq, inv_freq), dim=–1)

position = torch.arange(max_position_embeddings).float()

sinusoid_inp = torch.outer(position, inv_freq)

# save cosine and sine matrices as buffers

self.register_buffer(“cos”, sinusoid_inp.cos())

self.register_buffer(“sin”, sinusoid_inp.sin())

def forward(self, x: Tensor) -> Tensor:

“”“Apply RoPE to tensor x

Args:

x: Input tensor of shape (batch_size, seq_length, num_heads, head_dim)

Returns:

Output tensor of shape (batch_size, seq_length, num_heads, head_dim)

““”

batch_size, seq_len, num_heads, head_dim = x.shape

dtype = x.dtype

# transform the cosine and sine matrices to 4D tensor and the same dtype as x

cos = self.cos.to(dtype)[:seq_len].view(1, seq_len, 1, –1)

sin = self.sin.to(dtype)[:seq_len].view(1, seq_len, 1, –1)

# apply RoPE to x

output = (x * cos) + (rotate_half(x) * sin)

return output

The constructor of the RotaryPositionEncoding class uses a more sophisticated algorithm to compute the inv_freq tensor. The idea is to compute a wavelength for each frequency component, which represents the maximum distance between two tokens that the particular RoPE component can capture. If the wavelength is too short (or the frequency is too high), the frequency remains unchanged. However, if the wavelength is too long, the frequency is scaled down by the scale_factor, effectively lengthening the maximum distance that RoPE component can capture. To ensure stability, frequency components between the low and high frequency thresholds are smoothly interpolated.

To illustrate the effect of scaling, you can plot the resulting inverse frequency with Matplotlib:

import matplotlib.pyplot as plt

import torch

import math

N = 10_000.0

dim = 256

scale_factor = 8.0

low_factor, high_factor = 1.0, 4.0

base_length = 8192

# Compute the inverse frequency based on the standard RoPE formula

inv_freq = 1.0 / (N ** (torch.arange(0, dim, 2).float() / dim))

# Compute the modified inverse frequency

# scaled if freq too low, orig if freq too high, smoothed if in between

wavelen = 2 * math.pi / inv_freq

max_wavelen = base_length / low_factor

min_wavelen = base_length / high_factor

smooth_factor = (base_length / wavelen – low_factor) / (high_factor – low_factor)

smoothed = (1 – smooth_factor) * inv_freq / scale_factor + smooth_factor * inv_freq

new_freq = torch.where(wavelen > max_wavelen, inv_freq / scale_factor,

torch.where(wavelen < min_wavelen, inv_freq,

smoothed))

# Plot the resulting inverse frequency

plt.plot(inv_freq, label=‘Original’)

plt.plot(inv_freq / scale_factor, label=‘Scaled’)

plt.plot(new_freq, label=‘New Frequency’)

plt.grid(True)

plt.yscale(‘log’)

plt.xlabel(‘Dimension’)

plt.ylabel(‘Inverse Frequency’)

plt.legend()

plt.show()

The plot is shown below:

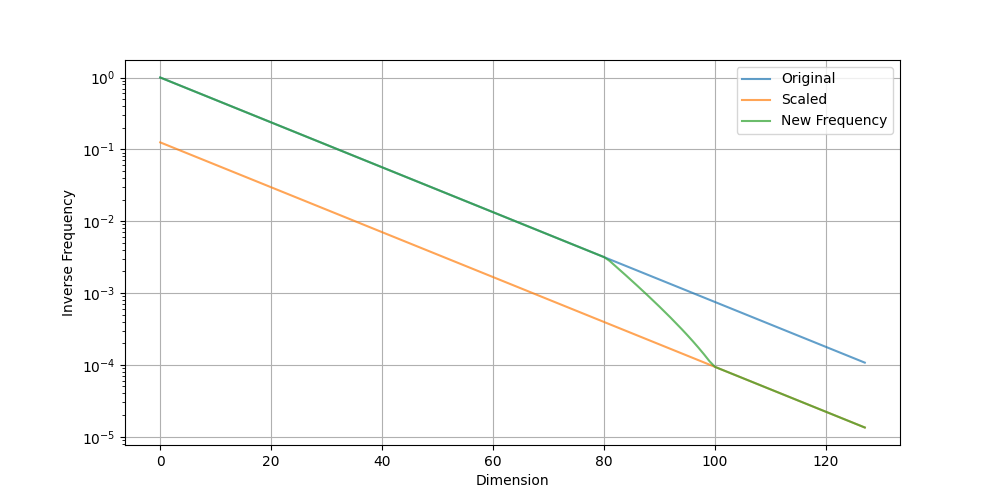
Plot of inverse frequency before and after RoPE scaling

You can see that the original RoPE frequency is preserved until the wavelength is approximately 2000 tokens (at an inverse frequency of around 0.003), after which it is gradually scaled. The wavelength is scaled by 8x when it exceeds 9000 tokens (the inverse frequency is below 6e-4).

From the x-axis of the plot, you can see that around 60% of the dimensions capture dependencies within 2000 tokens, while the rest capture distances up to 60000 tokens ($2pi N$ exactly; a larger $N$ enables the model to support longer context lengths).

This effectively provides a higher resolution for RoPE at short distances and a lower resolution at long distances, matching how language models should behave when understanding language.

Summary

In this article, you learned how RoPE is adapted for long context length. Specifically, you learned how Llama 3 supports longer context lengths by scaling the RoPE frequency at the low-frequency end.

Rotary Position Embeddings for Long Context Length

Overview

Simple RoPE

RoPE for Long Context Length

Further Reading

Summary

No comments yet.