Source: MachineLearningMastery.com
Tensor parallelism is a model-parallelism technique that shards a tensor along a specific dimension. It distributes the computation of a tensor across multiple devices with minimal communication overhead. This technique is suitable for models with very large parameter tensors where even a single matrix multiplication is too large to fit on a single GPU. In this article, you will learn how to use tensor parallelism. In particular, you will learn about:
- What is tensor parallelism
- How to design a tensor parallel plan
- How to apply tensor parallelism in PyTorch
Let’s get started!

Train Your Large Model on Multiple GPUs with Tensor Parallelism.
Photo by Seth kane. Some rights reserved.
Overview
This article is divided into five parts; they are:
- An Example of Tensor Parallelism
- Setting Up Tensor Parallelism
- Preparing Model for Tensor Parallelism
- Train a Model with Tensor Parallelism
- Combining Tensor Parallelism with FSDP
An Example of Tensor Parallelism
Tensor parallelism originated from the Megatron-LM paper. This technique does not apply to all operations; however, certain operations, such as matrix multiplication, are implemented with sharded computation.
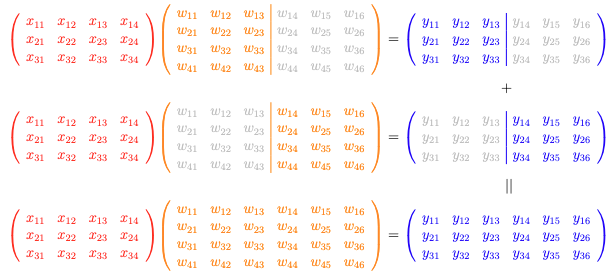
Column-wise tensor parallel: You sharded the weight $mathbf{W}$ into columns, and applied the matrix multiplication $mathbf{XW}=mathbf{Y}$ to produce sharded output that needs to be concatenated.
Let’s consider a simple matrix-matrix multiplication operation as follows:
It is a $3times 4$ matrix $mathbf{X}$ multiplied by a $4times 6$ matrix $mathbf{W}$ to produce a $3times 6$ matrix $mathbf{Y}$. You can indeed break it down into two matrix multiplications, one is $mathbf{X}$ times a $4times 3$ matrix $mathbf{W}_1$ to produce a $3times 3$ matrix $mathbf{Y}_1$, and the other is $mathbf{X}$ times another $3times 2$ matrix $mathbf{W}_2$ to produce a $3times 3$ matrix $mathbf{Y}_2$. Then the final $mathbf{Y}$ is the concatenation of $mathbf{Y}_1$ and $mathbf{Y}_2$.
You can see that in this case, you do not need to host the large matrix $mathbf{W}$ but work on a smaller split of it. This saves memory. The output of each split is smaller, hence it also communicates faster to other devices.
The case above is called column-wise parallel. You can generalize this to have more than two splits of the matrix $mathbf{W}$ along the column dimension.
Another variation is row-wise parallel, which is illustrated as follows:

Row-wise tensor parallel: You sharded the weight $mathbf{W}$ into rows, and applied the matrix multiplication $mathbf{XW}=mathbf{Y}$ to produce partial outputs that need to be added elementwise.
With the same $mathbf{XW}=mathbf{Y}$ matrix multiplication, you now split $mathbf{X}$ into columns and split $mathbf{W}$ into rows. In the illustration above, a $3times 2$ matrix from the left half of $mathbf{X}$ multiplies by a $2times 6$ matrix from the upper half of $mathbf{W}$ to produce a $3times 6$ matrix. The output shape is the same as the full equation, but the values only correspond to the upper half of $mathbf{W}$. Repeating the same operation with the right half of $mathbf{X}$ and the lower half of $mathbf{W}$, then summing the two results, gives you the final output $mathbf{Y}$.
In row-wise parallel, you work with splits of both $mathbf{X}$ and $mathbf{W}$. The workload is lighter than performing the full matrix multiplication. The output is larger than with column-wise parallel, requiring more bandwidth to communicate the result to other devices.
Not all operations in your deep learning model are matrix multiplications. Therefore, tensor parallelism does not work on every element in your model. Some operations, such as activation functions or normalization layers, can be parallelized differently. For operations that cannot be parallelized, your model must compute them in their original form.
Tensor parallelism offers benefits beyond memory savings—it provides fine-grained control over computation and communication patterns. Since matrix multiplications are sharded, you can control whether to unshard the result, allowing you to avoid communication overhead when working directly with sharded DTensor objects.
Setting Up Tensor Parallelism
Tensor parallelism in PyTorch is a part of the distributed framework. Therefore, the script is launched with torchrun command as in the case of distributed data parallelism, pipeline parallelism, and fully sharded data parallelism. You need to initialize the distributed environment as usual, but you also need to set up the device mesh:
|
import os import torch import torch.distributed as dist # Initialize the distributed environment dist.init_process_group(backend=“nccl”) local_rank = int(os.environ[“LOCAL_RANK”]) device = torch.device(f“cuda:{local_rank}”) rank = dist.get_rank() world_size = dist.get_world_size() # Initialize the mesh for tensor parallelism mesh = dist.device_mesh.init_device_mesh( “cuda”, (world_size,), ) |
The device mesh is a high-level abstraction of the process group. You will see why it is needed in later sections. It is necessary because you use the mesh to wrap a model into a tensor parallel model, using the following syntax:
|
from torch.distributed.tensor.parallel import parallelize_module model = parallelize_module(model, mesh, tp_plan) |
Afterward, some of the model’s weights will be replaced with DTensor objects, enabling operations to run in parallel. Distributed collective operations such as all-gather, all-reduce, and reduce-scatter may be performed internally to make the model work as if it were on a single device. These details are transparent to you.
Preparing Model for Tensor Parallelism
Let’s see how to run the training script from the previous article with tensor parallelism.
Converting a model to run with tensor parallelism does not require changing the model architecture. Instead, you need to know the fully-qualified name of each module and submodule in your model. These are the same as the keys in your model’s state_dict(), or you can revisit your model architecture code to find the module names.
You need to identify those names to create a parallelization plan. It is a Python dictionary that maps module names to ParallelStyle objects. Below is an example:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
tp_plan = { “input_layernorm”: SequenceParallel(), “self_attn”: PrepareModuleInput( input_layouts=Shard(dim=1), # only one position arg will be used desired_input_layouts=Replicate(), ), # Q/K/V output will be used with GQA, prefer to be replicated “self_attn.q_proj”: ColwiseParallel(output_layouts=Replicate()), “self_attn.k_proj”: ColwiseParallel(output_layouts=Replicate()), “self_attn.v_proj”: ColwiseParallel(output_layouts=Replicate()), “self_attn.o_proj”: RowwiseParallel(input_layouts=Replicate(), output_layouts=Shard(1)), “post_attention_layernorm”: SequenceParallel(), “mlp”: PrepareModuleInput( input_layouts=Shard(dim=1), desired_input_layouts=Replicate(), ), “mlp.gate_proj”: ColwiseParallel(), “mlp.up_proj”: ColwiseParallel(), “mlp.down_proj”: RowwiseParallel(output_layouts=Shard(1)), } with torch.device(“meta”): model_config = LlamaConfig() model = LlamaForPretraining(model_config) for layer in model.base_model.layers: parallelize_module(layer, mesh, tp_plan) |
The model architecture code is identical to that in the previous article. The dictionary tp_plan is created from the perspective of a transformer block. Note that each block is declared as:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
class LlamaAttention(nn.Module): def __init__(self, config: LlamaConfig) -> None: super().__init__() ... # Linear layers for Q, K, V projections self.q_proj = nn.Linear(self.hidden_size, self.num_heads * self.head_dim, bias=False) self.k_proj = nn.Linear(self.hidden_size, self.num_kv_heads * self.head_dim, bias=False) self.v_proj = nn.Linear(self.hidden_size, self.num_kv_heads * self.head_dim, bias=False) self.o_proj = nn.Linear(self.num_heads * self.head_dim, self.hidden_size, bias=False) ... class LlamaMLP(nn.Module): def __init__(self, config: LlamaConfig) -> None: super().__init__() self.gate_proj = nn.Linear(config.hidden_size, config.intermediate_size, bias=False) self.up_proj = nn.Linear(config.hidden_size, config.intermediate_size, bias=False) self.act_fn = F.silu # SwiGLU activation function self.down_proj = nn.Linear(config.intermediate_size, config.hidden_size, bias=False) ... class LlamaDecoderLayer(nn.Module): def __init__(self, config: LlamaConfig) -> None: super().__init__() self.input_layernorm = nn.RMSNorm(config.hidden_size, eps=1e–5) self.self_attn = LlamaAttention(config) self.post_attention_layernorm = nn.RMSNorm(config.hidden_size, eps=1e–5) self.mlp = LlamaMLP(config) ... |
From the perspective of the class LlamaDecoderLayer, you can find an nn.Linear layer as layer.mlp.gate_proj, hence you use the key mlp.gate_proj in the tp_plan dictionary to reference it.
When you use tensor parallelism, you should be aware that PyTorch does not know how to parallelize an arbitrary module, such as the custom module that you defined. But a few standard modules have concrete implementations of tensor parallelism:
nn.Linearandnn.Embedding: You can useColwiseParallelandRowwiseParallelto parallelize them. The operation is described above.nn.LayerNorm,nn.RMSNorm, andnn.Dropout: You can useSequenceParallelto parallelize them.
As PyTorch is evolving, refer to the official documentation for the latest coverage of tensor parallelism.
Once you set up tp_plan, you can apply it to the model using the parallelize_module() function. This replaces the module’s parameters with DTensor objects and makes the module run sharded computations as if it were on a single device. The for-loop above applies parallelize_module() to each transformer block for convenience. You can also apply it to the full base model, but you would need to update tp_plan with considerable repetition, since transformer blocks are repeated many times in the base model.
The transformer block contains two RMS norm layers. You mark them with SequenceParallel to indicate they should be sharded on the sequence dimension (dimension 1 of the input tensor).
The transformer block contains several nn.Linear layers: three in the feed-forward sublayer and four in the attention sublayer. You can mark them with either ColwiseParallel or RowwiseParallel to parallelize them, but there are some considerations:
ColwiseParallelby default expects a full tensor as input, and the output is sharded on the last dimension, making the output tensor smaller.RowwiseParallelby default expects a tensor sharded on the last dimension as input, and the output is a full-sized tensor, the same size as if it were not parallelized.
This is why you specify:
|
{ ... “mlp.gate_proj”: ColwiseParallel(), “mlp.up_proj”: ColwiseParallel(), “mlp.down_proj”: RowwiseParallel(output_layouts=Shard(1)), } |
In the feed-forward sublayer, you project the input tensor to $4times$ larger in the last dimension (using gate_proj and up_proj) and apply SwiGLU activation, then project the result back to the original size (using down_proj). Using ColwiseParallel for gate_proj and up_proj reduces the output tensor size and reduces communication overhead. You do not need to send the output to another device since the next layer, down_proj, uses RowwiseParallel and expects a tensor sharded on the last dimension as input—the output from ColwiseParallel fits perfectly. This demonstrates how to design a tensor parallel plan for your model.
The output from a RowwiseParallel layer defaults to a full-sized DTensor object, but you can change this requirement in the tp_plan for the down_proj layer to make it sharded on dimension 1. The tensor parallelism engine will determine the required communication operations. The reason for sharding on dimension 1 is that the next layer in the larger model is the RMS norm layer from the subsequent transformer block, and you need to prepare the tensor for that layer.
Adding input_layouts or output_layouts allows you to override the default behavior of ColwiseParallel and RowwiseParallel. This explains why you set the plan for the nn.Linear layers in the attention sublayer:
|
{ ... “self_attn.q_proj”: ColwiseParallel(output_layouts=Replicate()), “self_attn.k_proj”: ColwiseParallel(output_layouts=Replicate()), “self_attn.v_proj”: ColwiseParallel(output_layouts=Replicate()), “self_attn.o_proj”: RowwiseParallel(input_layouts=Replicate(), output_layouts=Shard(1)), } |
The Q/K/V projection outputs will be used with grouped-query attention (GQA). You use F.scaled_dot_product_attention() to compute the attention scores, but the way it is used in the LlamaAttention class, along with various tensor transpose and reshape operations, does not work well with distributed tensors. Therefore, you set the output to Replicate() to force a full copy to each device. Correspondingly, the input to o_proj will be a full tensor from the attention output, so you set input_layouts=Replicate(). Similarly, since the output from o_proj will be the input to the RMS norm, you set output_layouts=Shard(1) to make it compatible.
One more consideration: Since this is a pre-norm model, the inputs to the attention and feed-forward sublayers are outputs from the RMS norm, which are sharded on the sequence dimension. However, the first operation in both sublayers is a matrix multiplication with ColwiseParallel. You need to transform a tensor sharded on dimension 1 into a full tensor when passing it to the sublayers. This is why you use PrepareModuleInput to annotate the two sublayers:
|
{ ... “self_attn”: PrepareModuleInput( input_layouts=Shard(dim=1), # only one position arg will be used desired_input_layouts=Replicate(), ), “mlp”: PrepareModuleInput( input_layouts=Shard(dim=1), desired_input_layouts=Replicate(), ), } |
The attention sublayer is defined as follows:
|
... class LlamaAttention(nn.Module): ... def forward(self, hidden_states: Tensor, rope: RotaryPositionEncoding, attn_mask: Tensor) -> Tensor: ... class LlamaDecoderLayer(nn.Module): ... def forward(self, hidden_states: Tensor, rope: RotaryPositionEncoding, attn_mask: Tensor) -> Tensor: ... attn_outputs = self.self_attn(hidden_states, rope=rope, attn_mask=attn_mask) ... |
The forward() function of LlamaAttention takes three arguments. In LlamaDecoderLayer, you call the attention sublayer with hidden_states as a positional argument and rope and attn_mask as keyword arguments. If you were to use the LlamaAttention class with all keyword arguments, that is, self.self_attn(hidden_states=hidden_states, rope=rope, attn_mask=attn_mask), you would set input_kwarg_layouts and desired_input_kwarg_layouts instead of input_layouts and desired_input_layouts. Since your usage pattern has only one positional argument, you set input_layouts=Shard(dim=1) to indicate that you expect a DTensor sharded on dimension 1 as input.
There are also PrepareModuleOutput and PrepareModuleInputOutput if you need to override the DTensor layout in other cases.
Some other elements in the top-level model can be parallelized. So you can create a second plan and apply it to the top-level model:
|
tp_plan = { “base_model.embed_tokens”: RowwiseParallel( input_layouts=Replicate(), output_layouts=Shard(1), ), “base_model.norm”: SequenceParallel(), “lm_head”: ColwiseParallel( input_layouts=Shard(1), output_layouts=Replicate(), ), } parallelize_module(model, mesh, tp_plan) |
By now, your model is parallelized. You can check that is the case by verifying a special attribute on an element that is parallelized:
|
assert getattr(model.lm_head, “_distribute_module_applied”, False) |
Train a Model with Tensor Parallelism
That’s all you need for tensor parallelism. You set up the data loader, optimizer, learning rate scheduler, and loss function as usual, and nothing else needs to change in the training loop. It works because the input tensor is replicated across the mesh, and the embedding layer shards the tensor initially. As the input propagates through the model, it reaches the prediction head lm_head, which produces a replicated tensor as output. The loss can then be computed as usual, and gradient updates are applied to the DTensor objects.
However, you can go one step further by having the model produce a sharded tensor as output, then compute the loss on that tensor. This only works for cross-entropy loss using F.cross_entropy() or nn.CrossEntropyLoss(), which is the case here. You need to update the tensor parallel plan:
|
tp_plan = { “base_model.embed_tokens”: RowwiseParallel( input_layouts=Replicate(), output_layouts=Shard(1), ), “base_model.norm”: SequenceParallel(), “lm_head”: ColwiseParallel( input_layouts=Shard(1), # output_layouts=Replicate(), use_local_output=False, # use DTensor output ), } parallelize_module(model, mesh, tp_plan) |
Note that the output of the final layer, lm_head, uses ColwiseParallel with output_layouts set to the default, which is sharded along the last dimension. You also set use_local_output=False to keep the output as a DTensor object. In the training loop, you need to wrap the loss calculation as follows:
|
... from torch.distributed.tensor.parallel import loss_parallel for epoch in range(epochs): for batch in dataloader: ... logits = model(input_ids, attn_mask) optimizer.zero_grad() with loss_parallel(): # Compute loss: cross-entropy between logits and target, ignoring padding tokens loss = loss_fn(logits.view(–1, logits.size(–1)), target_ids.view(–1)) # Backward with loss loss.backward() optimizer.step() |
This way, you pass the reference tensor target_ids to each device in the tensor parallel device mesh, and each device computes its corresponding loss based on its shard of logits. The gradient is then computed from each shard in a parallelized backward pass. Once computed and stored as a sharded tensor, the optimizer updates the weights as usual.
The final piece of the training script involves saving and loading model checkpoints. Since you are running distributed training, use the distributed checkpointing API as mentioned in the previous article.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
def load_checkpoint(model: nn.Module, optimizer: torch.optim.Optimizer, scheduler: lr_scheduler.SequentialLR) -> None: dist.barrier() load( {“model”: model, “optimizer”: optimizer}, checkpoint_id=“checkpoint-dist”, planner=DefaultLoadPlanner(allow_partial_load=True), # ignore keys for RoPE buffer ) scheduler.load_state_dict( torch.load(“checkpoint-dist/lrscheduler.pt”, map_location=device), ) dist.barrier() def save_checkpoint(model: nn.Module, optimizer: torch.optim.Optimizer, scheduler: lr_scheduler.SequentialLR) -> None: dist.barrier() save( {“model”: model, “optimizer”: optimizer}, checkpoint_id=“checkpoint-dist”, ) if dist.get_rank() == 0: torch.save(scheduler.state_dict(), “checkpoint-dist/lrscheduler.pt”) dist.barrier() |
For completeness, below is the full script for running tensor parallelism training:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 |
import dataclasses import os import datasets import tokenizers import torch import torch.distributed as dist import torch.nn as nn import torch.nn.functional as F import torch.optim.lr_scheduler as lr_scheduler import tqdm from torch import Tensor from torch.distributed.checkpoint import load, save from torch.distributed.checkpoint.default_planner import DefaultLoadPlanner from torch.distributed.tensor import Replicate, Shard from torch.distributed.tensor.parallel import ( ColwiseParallel, PrepareModuleInput, RowwiseParallel, SequenceParallel, loss_parallel, parallelize_module, ) # Set default to bfloat16 torch.set_default_dtype(torch.bfloat16) # Build the model @dataclasses.dataclass class LlamaConfig: “”“Define Llama model hyperparameters.”“” vocab_size: int = 50000 # Size of the tokenizer vocabulary max_position_embeddings: int = 2048 # Maximum sequence length hidden_size: int = 768 # Dimension of hidden layers intermediate_size: int = 4*768 # Dimension of MLP’s hidden layer num_hidden_layers: int = 12 # Number of transformer layers num_attention_heads: int = 12 # Number of attention heads num_key_value_heads: int = 3 # Number of key-value heads for GQA # !! may conflict with TP size class RotaryPositionEncoding(nn.Module): “”“Rotary position encoding.”“” def __init__(self, dim: int, max_position_embeddings: int) -> None: “”“Initialize the RotaryPositionEncoding module. Args: dim: The hidden dimension of the input tensor to which RoPE is applied max_position_embeddings: The maximum sequence length of the input tensor ““” super().__init__() self.dim = dim self.max_position_embeddings = max_position_embeddings # compute a matrix of ntheta_i N = 10_000.0 inv_freq = 1.0 / (N ** (torch.arange(0, dim, 2) / dim)) inv_freq = torch.cat((inv_freq, inv_freq), dim=–1) position = torch.arange(max_position_embeddings) sinusoid_inp = torch.outer(position, inv_freq) # save cosine and sine matrices as buffers, not parameters self.register_buffer(“cos”, sinusoid_inp.cos()) self.register_buffer(“sin”, sinusoid_inp.sin()) def forward(self, x: Tensor) -> Tensor: “”“Apply RoPE to tensor x. Args: x: Input tensor of shape (batch_size, seq_length, num_heads, head_dim) Returns: Output tensor of shape (batch_size, seq_length, num_heads, head_dim) ““” batch_size, seq_len, num_heads, head_dim = x.shape device = x.device dtype = x.dtype # transform the cosine and sine matrices to 4D tensor and the same dtype as x cos = self.cos.to(device, dtype)[:seq_len].view(1, seq_len, 1, –1) sin = self.sin.to(device, dtype)[:seq_len].view(1, seq_len, 1, –1) # apply RoPE to x x1, x2 = x.chunk(2, dim=–1) rotated = torch.cat((–x2, x1), dim=–1) output = (x * cos) + (rotated * sin) return output class LlamaAttention(nn.Module): “”“Grouped-query attention with rotary embeddings.”“” def __init__(self, config: LlamaConfig) -> None: super().__init__() self.hidden_size = config.hidden_size self.num_heads = config.num_attention_heads self.head_dim = self.hidden_size // self.num_heads self.num_kv_heads = config.num_key_value_heads # GQA: H_kv < H_q # hidden_size must be divisible by num_heads assert (self.head_dim * self.num_heads) == self.hidden_size # Linear layers for Q, K, V projections self.q_proj = nn.Linear(self.hidden_size, self.num_heads * self.head_dim, bias=False) self.k_proj = nn.Linear(self.hidden_size, self.num_kv_heads * self.head_dim, bias=False) self.v_proj = nn.Linear(self.hidden_size, self.num_kv_heads * self.head_dim, bias=False) self.o_proj = nn.Linear(self.num_heads * self.head_dim, self.hidden_size, bias=False) def forward(self, hidden_states: Tensor, rope: RotaryPositionEncoding, attn_mask: Tensor) -> Tensor: bs, seq_len, dim = hidden_states.size() # Project inputs to Q, K, V query_states = self.q_proj(hidden_states).view(bs, seq_len, self.num_heads, self.head_dim) key_states = self.k_proj(hidden_states).view(bs, seq_len, self.num_kv_heads, self.head_dim) value_states = self.v_proj(hidden_states).view(bs, seq_len, self.num_kv_heads, self.head_dim) # Apply rotary position embeddings query_states = rope(query_states) key_states = rope(key_states) # Transpose tensors from BSHD to BHSD dimension for scaled_dot_product_attention query_states = query_states.transpose(1, 2) key_states = key_states.transpose(1, 2) value_states = value_states.transpose(1, 2) # Use PyTorch’s optimized attention implementation # setting is_causal=True is incompatible with setting explicit attention mask attn_output = F.scaled_dot_product_attention( query_states, key_states, value_states, attn_mask=attn_mask, dropout_p=0.0, enable_gqa=True, ) # Transpose output tensor from BHSD to BSHD dimension, reshape to 3D, and then project output attn_output = attn_output.transpose(1, 2).reshape(bs, seq_len, self.hidden_size) attn_output = self.o_proj(attn_output) return attn_output class LlamaMLP(nn.Module): “”“Feed-forward network with SwiGLU activation.”“” def __init__(self, config: LlamaConfig) -> None: super().__init__() # Two parallel projections for SwiGLU self.gate_proj = nn.Linear(config.hidden_size, config.intermediate_size, bias=False) self.up_proj = nn.Linear(config.hidden_size, config.intermediate_size, bias=False) self.act_fn = F.silu # SwiGLU activation function # Project back to hidden size self.down_proj = nn.Linear(config.intermediate_size, config.hidden_size, bias=False) def forward(self, x: Tensor) -> Tensor: # SwiGLU activation: multiply gate and up-projected inputs gate = self.act_fn(self.gate_proj(x)) up = self.up_proj(x) return self.down_proj(gate * up) class LlamaDecoderLayer(nn.Module): “”“Single transformer layer for a Llama model.”“” def __init__(self, config: LlamaConfig) -> None: super().__init__() self.input_layernorm = nn.RMSNorm(config.hidden_size, eps=1e–5) self.self_attn = LlamaAttention(config) self.post_attention_layernorm = nn.RMSNorm(config.hidden_size, eps=1e–5) self.mlp = LlamaMLP(config) def forward(self, hidden_states: Tensor, rope: RotaryPositionEncoding, attn_mask: Tensor) -> Tensor: # First residual block: Self-attention residual = hidden_states hidden_states = self.input_layernorm(hidden_states) attn_outputs = self.self_attn(hidden_states, rope=rope, attn_mask=attn_mask) hidden_states = attn_outputs + residual # Second residual block: MLP residual = hidden_states hidden_states = self.post_attention_layernorm(hidden_states) hidden_states = self.mlp(hidden_states) + residual return hidden_states class LlamaModel(nn.Module): “”“The full Llama model without any pretraining heads.”“” def __init__(self, config: LlamaConfig) -> None: super().__init__() self.rotary_emb = RotaryPositionEncoding( config.hidden_size // config.num_attention_heads, config.max_position_embeddings, ) self.embed_tokens = nn.Embedding(config.vocab_size, config.hidden_size) self.layers = nn.ModuleList([ LlamaDecoderLayer(config) for _ in range(config.num_hidden_layers) ]) self.norm = nn.RMSNorm(config.hidden_size, eps=1e–5) def forward(self, input_ids: Tensor, attn_mask: Tensor) -> Tensor: # Convert input token IDs to embeddings hidden_states = self.embed_tokens(input_ids) # Process through all transformer layers, then the final norm layer for layer in self.layers: hidden_states = layer(hidden_states, rope=self.rotary_emb, attn_mask=attn_mask) hidden_states = self.norm(hidden_states) # Return the final hidden states return hidden_states class LlamaForPretraining(nn.Module): def __init__(self, config: LlamaConfig) -> None: super().__init__() self.base_model = LlamaModel(config) self.lm_head = nn.Linear(config.hidden_size, config.vocab_size, bias=False) def forward(self, input_ids: Tensor, attn_mask: Tensor) -> Tensor: hidden_states = self.base_model(input_ids, attn_mask) return self.lm_head(hidden_states) def create_causal_mask(batch: Tensor, dtype: torch.dtype = torch.float32) -> Tensor: “”“Create a causal mask for self-attention. Args: batch: Batch of sequences, shape (batch_size, seq_len) dtype: Data type of the mask Returns: Causal mask of shape (seq_len, seq_len) ““” batch_size, seq_len = batch.shape mask = torch.full((seq_len, seq_len), float(“-inf”), device=batch.device, dtype=dtype) .triu(diagonal=1) return mask def create_padding_mask(batch: Tensor, padding_token_id: int, dtype: torch.dtype = torch.float32) -> Tensor: “”“Create a padding mask for a batch of sequences for self-attention. Args: batch: Batch of sequences, shape (batch_size, seq_len) padding_token_id: ID of the padding token dtype: Data type of the mask Returns: Padding mask of shape (batch_size, 1, seq_len, seq_len) ““” padded = torch.zeros_like(batch, device=batch.device, dtype=dtype) .masked_fill(batch == padding_token_id, float(“-inf”)) mask = padded[:,:,None] + padded[:,None,:] return mask[:, None, :, :] # Generator function to create padded sequences of fixed length class PretrainingDataset(torch.utils.data.Dataset): def __init__(self, dataset: datasets.Dataset, tokenizer: tokenizers.Tokenizer, seq_length: int): self.dataset = dataset self.tokenizer = tokenizer self.seq_length = seq_length self.bot = tokenizer.token_to_id(“[BOT]”) self.eot = tokenizer.token_to_id(“[EOT]”) self.pad = tokenizer.token_to_id(“[PAD]”) def __len__(self): return len(self.dataset) def __getitem__(self, index: int) -> tuple[Tensor, Tensor]: “”“Get a sequence of token ids from the dataset. [BOT] and [EOT] tokens are added. Clipped and padded to the sequence length. ““” seq = self.dataset[index][“text”] tokens: list[int] = [self.bot] + self.tokenizer.encode(seq).ids + [self.eot] # pad to target sequence length toklen = len(tokens) if toklen < self.seq_length+1: pad_length = self.seq_length+1 – toklen tokens += [self.pad] * pad_length # return the sequence x = torch.tensor(tokens[:self.seq_length], dtype=torch.int64) y = torch.tensor(tokens[1:self.seq_length+1], dtype=torch.int64) return x, y def load_checkpoint(model: nn.Module, optimizer: torch.optim.Optimizer, scheduler: lr_scheduler.SequentialLR) -> None: dist.barrier() load( {“model”: model, “optimizer”: optimizer}, checkpoint_id=“checkpoint-dist”, planner=DefaultLoadPlanner(allow_partial_load=True), # ignore keys for RoPE buffer ) scheduler.load_state_dict( torch.load(“checkpoint-dist/lrscheduler.pt”, map_location=device), ) dist.barrier() def save_checkpoint(model: nn.Module, optimizer: torch.optim.Optimizer, scheduler: lr_scheduler.SequentialLR) -> None: dist.barrier() save( {“model”: model, “optimizer”: optimizer}, checkpoint_id=“checkpoint-dist”, ) if dist.get_rank() == 0: torch.save(scheduler.state_dict(), “checkpoint-dist/lrscheduler.pt”) dist.barrier() # Load the tokenizer and dataset tokenizer = tokenizers.Tokenizer.from_file(“bpe_50K.json”) dataset = datasets.load_dataset(“HuggingFaceFW/fineweb”, “sample-10BT”, split=“train”) # Initialize the distributed environment dist.init_process_group(backend=“nccl”) local_rank = int(os.environ[“LOCAL_RANK”]) device = torch.device(f“cuda:{local_rank}”) rank = dist.get_rank() world_size = dist.get_world_size() print(f“World size {world_size}, rank {rank}, local rank {local_rank}. Using {device}”) # Initialize the mesh for tensor parallelism mesh = dist.device_mesh.init_device_mesh( “cuda”, (world_size,), ) print(f“({rank}) Mesh: {mesh}, TP size: {mesh.size()}, TP local rank: {mesh.get_local_rank()}”) # Create pretraining model on meta device, on all ranks with torch.device(“meta”): model_config = LlamaConfig() model = LlamaForPretraining(model_config) # Set up tensor parallelism on each transformer block in the base model tp_plan = { “input_layernorm”: SequenceParallel(), “self_attn”: PrepareModuleInput( input_layouts=Shard(dim=1), # only one position arg will be used desired_input_layouts=Replicate(), ), # Q/K projections output will be used with RoPE, need to be replicated # Q/K/V output will be used with attention, also need to be replicated “self_attn.q_proj”: ColwiseParallel(output_layouts=Replicate()), “self_attn.k_proj”: ColwiseParallel(output_layouts=Replicate()), “self_attn.v_proj”: ColwiseParallel(output_layouts=Replicate()), “self_attn.o_proj”: RowwiseParallel(input_layouts=Replicate(), output_layouts=Shard(1)), “post_attention_layernorm”: SequenceParallel(), “mlp”: PrepareModuleInput( input_layouts=Shard(dim=1), desired_input_layouts=Replicate(), ), “mlp.gate_proj”: ColwiseParallel(), “mlp.up_proj”: ColwiseParallel(), “mlp.down_proj”: RowwiseParallel(output_layouts=Shard(1)), } for layer in model.base_model.layers: layer = parallelize_module(layer, mesh, tp_plan) # Set up tensor parallelism on the embedding and output norm layers in the base model # and the prediction head in the top-level model tp_plan = { “base_model.embed_tokens”: RowwiseParallel( input_layouts=Replicate(), output_layouts=Shard(1), ), “base_model.norm”: SequenceParallel(), “lm_head”: ColwiseParallel( input_layouts=Shard(1), # output_layouts=Replicate(), # if not using loss parallel use_local_output=False, # Keep DTensor output for loss parallel ), } parallelize_module(model, mesh, tp_plan) def reset_all_weights(model: nn.Module) -> None: “”“Initialize all weights of the model after moving it away from meta device.”“” @torch.no_grad() def weight_reset(m: nn.Module): reset_parameters = getattr(m, “reset_parameters”, None) if callable(reset_parameters): m.reset_parameters() # Applies fn recursively to model itself and all of model.children() model.apply(fn=weight_reset) torch.manual_seed(42) model.to_empty(device=device) reset_all_weights(model) print(f“({rank}) Model:n{model}”) # Training parameters epochs = 3 learning_rate = 1e–3 batch_size = 32 seq_length = 512 num_warmup_steps = 1000 PAD_TOKEN_ID = tokenizer.token_to_id(“[PAD]”) model.train() # DataLoader, optimizer, scheduler, and loss function # Sampler is needed to shard the dataset across world size dataset = PretrainingDataset(dataset, tokenizer, seq_length) dataloader = torch.utils.data.DataLoader( dataset, batch_size=batch_size, pin_memory=True, # optional shuffle=False, num_workers=2, prefetch_factor=2, ) num_training_steps = len(dataloader) * epochs optimizer = torch.optim.AdamW( model.parameters(), lr=learning_rate, betas=(0.9, 0.99), eps=1e–8, weight_decay=0.1, ) warmup_scheduler = lr_scheduler.LinearLR( optimizer, start_factor=0.1, end_factor=1.0, total_iters=num_warmup_steps, ) cosine_scheduler = lr_scheduler.CosineAnnealingLR( optimizer, T_max=num_training_steps – num_warmup_steps, eta_min=0, ) scheduler = lr_scheduler.SequentialLR( optimizer, schedulers=[warmup_scheduler, cosine_scheduler], milestones=[num_warmup_steps], ) loss_fn = nn.CrossEntropyLoss(ignore_index=PAD_TOKEN_ID) # if checkpoint-dist dir exists, load the checkpoint to model and optimizer if os.path.exists(“checkpoint-dist”): load_checkpoint(model, optimizer, scheduler) # start training for epoch in range(epochs): pbar = tqdm.tqdm(dataloader, desc=f“({rank}) Epoch {epoch+1}/{epochs}”) for batch_id, batch in enumerate(pbar): if batch_id % 1000 == 0: save_checkpoint(model, optimizer, scheduler) # Get batched data, move to device input_ids, target_ids = batch input_ids = input_ids.to(device) target_ids = target_ids.to(device) # create attention mask: causal mask + padding mask attn_mask = create_causal_mask(input_ids) + create_padding_mask(input_ids, PAD_TOKEN_ID) # Extract output from model logits = model(input_ids, attn_mask) optimizer.zero_grad() with loss_parallel(): # Compute loss: cross-entropy between logits and target, ignoring padding tokens loss = loss_fn(logits.view(–1, logits.size(–1)), target_ids.view(–1)) # Backward with loss on DTensor loss.backward() torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0) optimizer.step() scheduler.step() pbar.set_postfix(loss=loss.item()) pbar.update(1) pbar.close() # Save the model save_checkpoint(model, optimizer, scheduler) # Clean up the distributed environment dist.destroy_process_group() |
You should run this code with torchrun command such as:
|
torchrun —standalone —nproc_per_node=4 train.py |
Combining Tensor Parallelism with FSDP
Tensor parallelism is a form of model parallelism: the model runs separately on each device, with distinct operations. Data parallelism replicates the model across multiple devices, each performing the same operations on different data.
You can combine tensor parallelism with data parallelism to achieve 2D parallelism. It is straightforward to integrate with FSDP with only a few lines of code.
Before you begin, you must determine how tensor parallelism and data parallelism should work together. This is called 2D parallelism because you can consider your GPU cluster as a 2D grid:
$$
begin{bmatrix}
text{GPU}(0,0) & text{GPU}(0,1) \
text{GPU}(1,0) & text{GPU}(1,1) \
end{bmatrix}
$$
You now number each device as a pair of indices, such as $(0,1)$. The first index is usually the data-parallel index, and the second is the tensor-parallel index. If you have multiple GPUs across multiple nodes, the first index typically represents the node index, and the second represents the GPU index on that node. This is why it’s called a device mesh. You can define a mesh for 2D parallelism as follows:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
dist.init_process_group(backend=“nccl”, timeout=datetime.timedelta(seconds=60)) local_rank = int(os.environ[“LOCAL_RANK”]) device = torch.device(f“cuda:{local_rank}”) rank = dist.get_rank() world_size = dist.get_world_size() print(f“World size {world_size}, rank {rank}, local rank {local_rank}. Using {device}”) n_tensor_parallel = 2 assert world_size % n_tensor_parallel == 0, “Expect world size to be divisible by number of tensor parallel GPUs” mesh = dist.device_mesh.init_device_mesh( “cuda”, (world_size // n_tensor_parallel, n_tensor_parallel), mesh_dim_names=(“dp”, “tp”), ) print(f“({rank}) Mesh: {mesh}, “ f“DP size: {mesh[‘dp’].size()}, TP size: {mesh[‘tp’].size()}, “ f“DP local rank: {mesh[‘dp’].get_local_rank()}, “ f“TP local rank: {mesh[‘tp’].get_local_rank()}”) |
With this mesh, you apply tensor parallelism only to the tensor-parallel dimension. You can do this by using a submesh with parallelize_module() as follows:
|
parallelize_module(model, mesh[‘tp’], tp_plan) |
After converting the model to a tensor parallel model, you can further apply FSDP using the data parallel dimension submesh:
|
model = fully_shard(model, mesh=mesh[‘dp’]) |
This is essentially an FSDP model, so you need to set up the data loader accordingly using a DistributedSampler:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
batch_size = 64 // mesh[“dp”].size() dataset = PretrainingDataset(dataset, tokenizer, seq_length) sampler = DistributedSampler( dataset, shuffle=False, drop_last=True, num_replicas=mesh[“dp”].size(), rank=mesh[“dp”].get_local_rank(), ) dataloader = torch.utils.data.DataLoader( dataset, sampler=sampler, batch_size=batch_size, pin_memory=True, # optional shuffle=False, num_workers=2, prefetch_factor=2, ) |
Note that the DistributedSampler is repeated as many times as the data parallel size. Correspondingly, the batch_size is divided by the same number to maintain the same effective batch size.
The rest of the training script remains the same. Here’s how it works: When you pass a micro-batch of data to the model, it operates as an FSDP model, with each shard exchanging weights to create a temporary, unsharded model for processing. The FSDP model output is then combined to compute the loss.
Within the FSDP model, a tensor-parallel model is distributed across multiple devices. This device set is orthogonal to the FSDP dimension, and each FSDP shard forms a full tensor-parallel model. Each micro-batch is processed by the tensor-parallel model, in which each shard produces only a sharded output rather than a full output. You need to use all-gather to combine the sharded output or use loss parallelism to compute the loss on the sharded output.
In 2D parallelism, your model runs with two hierarchical levels of parallelism: first data parallelism, then tensor parallelism. The mesh design typically makes the first dimension (data parallel) inter-node and the second dimension (tensor parallel) intra-node to optimize performance. You can also replace FSDP with standard distributed data parallelism for a different 2D parallelism implementation. You can even create 3D parallelism by combining data, pipeline, and tensor parallelism in this hierarchical order, resulting in a 3D mesh grid.
For completeness, below is the full script for running 2D parallelism training using tensor parallelism and FSDP, and you still need to run it with torchrun:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 403 404 405 406 407 408 409 410 411 412 413 414 415 416 417 418 419 420 421 422 423 424 425 426 427 428 429 430 431 432 433 434 435 436 437 438 439 440 441 442 443 444 445 446 447 448 449 450 451 452 453 454 455 456 457 458 459 460 461 462 463 464 465 466 467 468 469 470 471 472 473 474 475 476 477 478 479 480 481 482 483 484 485 486 487 488 489 |
import dataclasses import datetime import os import datasets import tokenizers import torch import torch.distributed as dist import torch.nn as nn import torch.nn.functional as F import torch.optim.lr_scheduler as lr_scheduler import tqdm from torch import Tensor from torch.distributed.checkpoint import load, save from torch.distributed.checkpoint.default_planner import DefaultLoadPlanner from torch.distributed.fsdp import FSDPModule, fully_shard from torch.distributed.tensor import Replicate, Shard from torch.distributed.tensor.parallel import ( ColwiseParallel, PrepareModuleInput, RowwiseParallel, SequenceParallel, loss_parallel, parallelize_module, ) from torch.utils.data.distributed import DistributedSampler # Set default to bfloat16 torch.set_default_dtype(torch.bfloat16) print(“NCCL version:”, torch.cuda.nccl.version()) # Build the model @dataclasses.dataclass class LlamaConfig: “”“Define Llama model hyperparameters.”“” vocab_size: int = 50000 # Size of the tokenizer vocabulary max_position_embeddings: int = 2048 # Maximum sequence length hidden_size: int = 768 # Dimension of hidden layers intermediate_size: int = 4*768 # Dimension of MLP’s hidden layer num_hidden_layers: int = 12 # Number of transformer layers num_attention_heads: int = 12 # Number of attention heads num_key_value_heads: int = 3 # Number of key-value heads for GQA class RotaryPositionEncoding(nn.Module): “”“Rotary position encoding.”“” def __init__(self, dim: int, max_position_embeddings: int) -> None: “”“Initialize the RotaryPositionEncoding module. Args: dim: The hidden dimension of the input tensor to which RoPE is applied max_position_embeddings: The maximum sequence length of the input tensor ““” super().__init__() self.dim = dim self.max_position_embeddings = max_position_embeddings # compute a matrix of ntheta_i N = 10_000.0 inv_freq = 1.0 / (N ** (torch.arange(0, dim, 2) / dim)) inv_freq = torch.cat((inv_freq, inv_freq), dim=–1) position = torch.arange(max_position_embeddings) sinusoid_inp = torch.outer(position, inv_freq) # save cosine and sine matrices as buffers, not parameters self.register_buffer(“cos”, sinusoid_inp.cos()) self.register_buffer(“sin”, sinusoid_inp.sin()) def forward(self, x: Tensor) -> Tensor: “”“Apply RoPE to tensor x. Args: x: Input tensor of shape (batch_size, seq_length, num_heads, head_dim) Returns: Output tensor of shape (batch_size, seq_length, num_heads, head_dim) ““” batch_size, seq_len, num_heads, head_dim = x.shape device = x.device dtype = x.dtype # transform the cosine and sine matrices to 4D tensor and the same dtype as x cos = self.cos.to(device, dtype)[:seq_len].view(1, seq_len, 1, –1) sin = self.sin.to(device, dtype)[:seq_len].view(1, seq_len, 1, –1) # apply RoPE to x x1, x2 = x.chunk(2, dim=–1) rotated = torch.cat((–x2, x1), dim=–1) output = (x * cos) + (rotated * sin) return output class LlamaAttention(nn.Module): “”“Grouped-query attention with rotary embeddings.”“” def __init__(self, config: LlamaConfig) -> None: super().__init__() self.hidden_size = config.hidden_size self.num_heads = config.num_attention_heads self.head_dim = self.hidden_size // self.num_heads self.num_kv_heads = config.num_key_value_heads # GQA: H_kv < H_q # hidden_size must be divisible by num_heads assert (self.head_dim * self.num_heads) == self.hidden_size # Linear layers for Q, K, V projections self.q_proj = nn.Linear(self.hidden_size, self.num_heads * self.head_dim, bias=False) self.k_proj = nn.Linear(self.hidden_size, self.num_kv_heads * self.head_dim, bias=False) self.v_proj = nn.Linear(self.hidden_size, self.num_kv_heads * self.head_dim, bias=False) self.o_proj = nn.Linear(self.num_heads * self.head_dim, self.hidden_size, bias=False) def forward(self, hidden_states: Tensor, rope: RotaryPositionEncoding, attn_mask: Tensor) -> Tensor: bs, seq_len, dim = hidden_states.size() # Project inputs to Q, K, V query_states = self.q_proj(hidden_states).view(bs, seq_len, self.num_heads, self.head_dim) key_states = self.k_proj(hidden_states).view(bs, seq_len, self.num_kv_heads, self.head_dim) value_states = self.v_proj(hidden_states).view(bs, seq_len, self.num_kv_heads, self.head_dim) # Apply rotary position embeddings query_states = rope(query_states) key_states = rope(key_states) # Transpose tensors from BSHD to BHSD dimension for scaled_dot_product_attention query_states = query_states.transpose(1, 2) key_states = key_states.transpose(1, 2) value_states = value_states.transpose(1, 2) # Use PyTorch’s optimized attention implementation # setting is_causal=True is incompatible with setting explicit attention mask attn_output = F.scaled_dot_product_attention( query_states, key_states, value_states, attn_mask=attn_mask, dropout_p=0.0, enable_gqa=True, ) # Transpose output tensor from BHSD to BSHD dimension, reshape to 3D, and then project output attn_output = attn_output.transpose(1, 2).reshape(bs, seq_len, self.hidden_size) attn_output = self.o_proj(attn_output) return attn_output class LlamaMLP(nn.Module): “”“Feed-forward network with SwiGLU activation.”“” def __init__(self, config: LlamaConfig) -> None: super().__init__() # Two parallel projections for SwiGLU self.gate_proj = nn.Linear(config.hidden_size, config.intermediate_size, bias=False) self.up_proj = nn.Linear(config.hidden_size, config.intermediate_size, bias=False) self.act_fn = F.silu # SwiGLU activation function # Project back to hidden size self.down_proj = nn.Linear(config.intermediate_size, config.hidden_size, bias=False) def forward(self, x: Tensor) -> Tensor: # SwiGLU activation: multiply gate and up-projected inputs gate = self.act_fn(self.gate_proj(x)) up = self.up_proj(x) return self.down_proj(gate * up) class LlamaDecoderLayer(nn.Module): “”“Single transformer layer for a Llama model.”“” def __init__(self, config: LlamaConfig) -> None: super().__init__() self.input_layernorm = nn.RMSNorm(config.hidden_size, eps=1e–5) self.self_attn = LlamaAttention(config) self.post_attention_layernorm = nn.RMSNorm(config.hidden_size, eps=1e–5) self.mlp = LlamaMLP(config) def forward(self, hidden_states: Tensor, rope: RotaryPositionEncoding, attn_mask: Tensor) -> Tensor: # First residual block: Self-attention residual = hidden_states hidden_states = self.input_layernorm(hidden_states) attn_outputs = self.self_attn(hidden_states, rope=rope, attn_mask=attn_mask) hidden_states = attn_outputs + residual # Second residual block: MLP residual = hidden_states hidden_states = self.post_attention_layernorm(hidden_states) hidden_states = self.mlp(hidden_states) + residual return hidden_states class LlamaModel(nn.Module): “”“The full Llama model without any pretraining heads.”“” def __init__(self, config: LlamaConfig) -> None: super().__init__() self.rotary_emb = RotaryPositionEncoding( config.hidden_size // config.num_attention_heads, config.max_position_embeddings, ) self.embed_tokens = nn.Embedding(config.vocab_size, config.hidden_size) self.layers = nn.ModuleList([ LlamaDecoderLayer(config) for _ in range(config.num_hidden_layers) ]) self.norm = nn.RMSNorm(config.hidden_size, eps=1e–5) def forward(self, input_ids: Tensor, attn_mask: Tensor) -> Tensor: # Convert input token IDs to embeddings hidden_states = self.embed_tokens(input_ids) # Process through all transformer layers, then the final norm layer for layer in self.layers: hidden_states = layer(hidden_states, rope=self.rotary_emb, attn_mask=attn_mask) hidden_states = self.norm(hidden_states) # Return the final hidden states return hidden_states class LlamaForPretraining(nn.Module): def __init__(self, config: LlamaConfig) -> None: super().__init__() self.base_model = LlamaModel(config) self.lm_head = nn.Linear(config.hidden_size, config.vocab_size, bias=False) def forward(self, input_ids: Tensor, attn_mask: Tensor) -> Tensor: hidden_states = self.base_model(input_ids, attn_mask) return self.lm_head(hidden_states) def create_causal_mask(batch: Tensor, dtype: torch.dtype = torch.float32) -> Tensor: “”“Create a causal mask for self-attention. Args: batch: Batch of sequences, shape (batch_size, seq_len) dtype: Data type of the mask Returns: Causal mask of shape (seq_len, seq_len) ““” batch_size, seq_len = batch.shape mask = torch.full((seq_len, seq_len), float(“-inf”), device=batch.device, dtype=dtype) .triu(diagonal=1) return mask def create_padding_mask(batch: Tensor, padding_token_id: int, dtype: torch.dtype = torch.float32) -> Tensor: “”“Create a padding mask for a batch of sequences for self-attention. Args: batch: Batch of sequences, shape (batch_size, seq_len) padding_token_id: ID of the padding token dtype: Data type of the mask Returns: Padding mask of shape (batch_size, 1, seq_len, seq_len) ““” padded = torch.zeros_like(batch, device=batch.device, dtype=dtype) .masked_fill(batch == padding_token_id, float(“-inf”)) mask = padded[:,:,None] + padded[:,None,:] return mask[:, None, :, :] # Generator function to create padded sequences of fixed length class PretrainingDataset(torch.utils.data.Dataset): def __init__(self, dataset: datasets.Dataset, tokenizer: tokenizers.Tokenizer, seq_length: int): self.dataset = dataset self.tokenizer = tokenizer self.seq_length = seq_length self.bot = tokenizer.token_to_id(“[BOT]”) self.eot = tokenizer.token_to_id(“[EOT]”) self.pad = tokenizer.token_to_id(“[PAD]”) def __len__(self): return len(self.dataset) def __getitem__(self, index: int) -> tuple[Tensor, Tensor]: “”“Get a sequence of token ids from the dataset. [BOT] and [EOT] tokens are added. Clipped and padded to the sequence length. ““” seq = self.dataset[index][“text”] tokens: list[int] = [self.bot] + self.tokenizer.encode(seq).ids + [self.eot] # pad to target sequence length toklen = len(tokens) if toklen < self.seq_length+1: pad_length = self.seq_length+1 – toklen tokens += [self.pad] * pad_length # return the sequence x = torch.tensor(tokens[:self.seq_length], dtype=torch.int64) y = torch.tensor(tokens[1:self.seq_length+1], dtype=torch.int64) return x, y def load_checkpoint(model: nn.Module, optimizer: torch.optim.Optimizer, scheduler: lr_scheduler.SequentialLR) -> None: dist.barrier() load( {“model”: model, “optimizer”: optimizer}, checkpoint_id=“checkpoint-dist”, planner=DefaultLoadPlanner(allow_partial_load=True), # ignore keys for RoPE buffer ) scheduler.load_state_dict( torch.load(“checkpoint-dist/lrscheduler.pt”, map_location=device), ) dist.barrier() def save_checkpoint(model: nn.Module, optimizer: torch.optim.Optimizer, scheduler: lr_scheduler.SequentialLR) -> None: dist.barrier() save( {“model”: model, “optimizer”: optimizer}, checkpoint_id=“checkpoint-dist”, ) if dist.get_rank() == 0: torch.save(scheduler.state_dict(), “checkpoint-dist/lrscheduler.pt”) dist.barrier() # Load the tokenizer and dataset tokenizer = tokenizers.Tokenizer.from_file(“bpe_50K.json”) dataset = datasets.load_dataset(“HuggingFaceFW/fineweb”, “sample-10BT”, split=“train”) # Initialize the distributed environment dist.init_process_group(backend=“nccl”, timeout=datetime.timedelta(seconds=60)) local_rank = int(os.environ[“LOCAL_RANK”]) device = torch.device(f“cuda:{local_rank}”) rank = dist.get_rank() world_size = dist.get_world_size() print(f“World size {world_size}, rank {rank}, local rank {local_rank}. Using {device}”) # Initialize the mesh for tensor parallelism n_tensor_parallel = 2 assert world_size % n_tensor_parallel == 0, “Expect world size to be divisible by number of tensor parallel GPUs” mesh = dist.device_mesh.init_device_mesh( “cuda”, (world_size // n_tensor_parallel, n_tensor_parallel), mesh_dim_names=(“dp”, “tp”), ) print(f“({rank}) Mesh: {mesh}, DP size: {mesh[‘dp’].size()}, TP size: {mesh[‘tp’].size()}, DP local rank: {mesh[‘dp’].get_local_rank()}, TP local rank: {mesh[‘tp’].get_local_rank()}”) # Create pretraining model on meta device, on all ranks with torch.device(“meta”): model_config = LlamaConfig() model = LlamaForPretraining(model_config) # Set up tensor parallelism on each transformer block in the base model tp_plan = { “input_layernorm”: SequenceParallel(), “self_attn”: PrepareModuleInput( input_layouts=Shard(dim=1), # only one position arg will be used desired_input_layouts=Replicate(), ), # Q/K projections output will be used with RoPE, need to be replicated # Q/K/V output will be used with GQA, also need to be replicated “self_attn.q_proj”: ColwiseParallel(output_layouts=Replicate()), “self_attn.k_proj”: ColwiseParallel(output_layouts=Replicate()), “self_attn.v_proj”: ColwiseParallel(output_layouts=Replicate()), “self_attn.o_proj”: RowwiseParallel(input_layouts=Replicate(), output_layouts=Shard(1)), “post_attention_layernorm”: SequenceParallel(), “mlp”: PrepareModuleInput( input_layouts=Shard(dim=1), desired_input_layouts=Replicate(), ), “mlp.gate_proj”: ColwiseParallel(), “mlp.up_proj”: ColwiseParallel(), “mlp.down_proj”: RowwiseParallel(output_layouts=Shard(1)), } for layer in model.base_model.layers: parallelize_module(layer, mesh[“tp”], tp_plan) # Set up tensor parallelism on the embedding and output norm layers in the base model # and the prediction head in the top-level model tp_plan = { “base_model.embed_tokens”: RowwiseParallel( input_layouts=Replicate(), output_layouts=Shard(1), ), “base_model.norm”: SequenceParallel(), “lm_head”: ColwiseParallel( input_layouts=Shard(1), # output_layouts=Replicate(), # only if not using loss parallel use_local_output=False, # Keep DTensor output for loss parallel ), } parallelize_module(model, mesh[“tp”], tp_plan) # Convert tensor-parallelized model to FSDP2, must shard every component # shard across the “dp” dimension of the mesh for layer in model.base_model.layers: fully_shard(layer, mesh=mesh[“dp”]) fully_shard(model.base_model, mesh=mesh[“dp”]) fully_shard(model, mesh=mesh[“dp”]) def reset_all_weights(model: nn.Module) -> None: “”“Initialize all weights of the model after moving it away from meta device.”“” @torch.no_grad() def weight_reset(m: nn.Module): reset_parameters = getattr(m, “reset_parameters”, None) if callable(reset_parameters): m.reset_parameters() # Applies fn recursively to model itself and all of model.children() model.apply(fn=weight_reset) torch.manual_seed(42) model.to_empty(device=device) reset_all_weights(model) assert isinstance(model, FSDPModule), f“Expected FSDPModule, got {type(model)}” # Training parameters epochs = 3 learning_rate = 1e–3 batch_size = 64 // mesh[“dp”].size() seq_length = 512 num_warmup_steps = 1000 PAD_TOKEN_ID = tokenizer.token_to_id(“[PAD]”) model.train() # DataLoader, optimizer, scheduler, and loss function # Sampler is needed to shard the dataset across world size dataset = PretrainingDataset(dataset, tokenizer, seq_length) sampler = DistributedSampler( dataset, shuffle=False, drop_last=True, num_replicas=mesh[“dp”].size(), rank=mesh[“dp”].get_local_rank(), ) dataloader = torch.utils.data.DataLoader( dataset, sampler=sampler, batch_size=batch_size, pin_memory=True, # optional shuffle=False, num_workers=2, prefetch_factor=2, ) num_training_steps = len(dataloader) * epochs optimizer = torch.optim.AdamW( model.parameters(), lr=learning_rate, betas=(0.9, 0.99), eps=1e–8, weight_decay=0.1, ) warmup_scheduler = lr_scheduler.LinearLR( optimizer, start_factor=0.1, end_factor=1.0, total_iters=num_warmup_steps, ) cosine_scheduler = lr_scheduler.CosineAnnealingLR( optimizer, T_max=num_training_steps – num_warmup_steps, eta_min=0, ) scheduler = lr_scheduler.SequentialLR( optimizer, schedulers=[warmup_scheduler, cosine_scheduler], milestones=[num_warmup_steps], ) loss_fn = nn.CrossEntropyLoss(ignore_index=PAD_TOKEN_ID) # if checkpoint-dist dir exists, load the checkpoint to model and optimizer if os.path.exists(“checkpoint-dist”): load_checkpoint(model, optimizer, scheduler) # start training print(f“({rank}) Starting training”) for epoch in range(epochs): pbar = tqdm.tqdm(dataloader, desc=f“({rank}) Epoch {epoch+1}/{epochs}”) for batch_id, batch in enumerate(pbar): if batch_id % 1000 == 0: save_checkpoint(model, optimizer, scheduler) # Explicit prefetching before sending any data to model model.unshard() # Get batched data, move from CPU to GPU input_ids, target_ids = batch input_ids = input_ids.to(device) target_ids = target_ids.to(device) # create attention mask: causal mask + padding mask attn_mask = create_causal_mask(input_ids) + create_padding_mask(input_ids, PAD_TOKEN_ID) # Extract output from model logits = model(input_ids, attn_mask) optimizer.zero_grad() with loss_parallel(): # Compute loss: cross-entropy between logits and target, ignoring padding tokens loss = loss_fn(logits.view(–1, logits.size(–1)), target_ids.view(–1)) # Backward with loss on DTensor loss.backward() torch.nn.utils.clip_grad_norm_(model.parameters(), 1.0) optimizer.step() scheduler.step() pbar.set_postfix(loss=loss.item()) pbar.update(1) pbar.close() # Save the model save_checkpoint(model, optimizer, scheduler) # Clean up the distributed environment dist.destroy_process_group() |
Further Readings
Below are some resources that you may find useful:
- Shoeybi et al (2019) Megatron-LM: Training Multi-Billion Parameter Language Models Using Model Parallelism
- Getting Started with DeviceMesh, from PyTorch recipes
- Phillip Lippe (2022) Tensor Parallelism, UvA DL Notebooks
- Phillip Lippe (2022) Language Modeling with 3D Parallelism, UvA DL Notebooks
- Tensor Parallelism, from Glossary of Lightning AI documentation
- Tensor Parallel and 2D Parallel, example code from PyTorch Lightning
- Tensor Parallelism – torch.distributed.tensor.parallel API, from PyTorch documentation
- torch.utils.data.distributed.DistributedSampler API, from PyTorch documentation
- PyTorch native Tensor Parallel for Distributed Training, from PyTorch examples
Summary
In this article, you learned about tensor parallelism and how to use it in PyTorch. Specifically, you learned:
- Tensor parallelism is a model-parallelism technique that shards tensors along a specific dimension, enabling finer control over computation and communication patterns.
- You need to design a tensor-parallel plan to enable tensor parallelism. Only a few standard modules can be parallelized.
- You can combine tensor parallelism with FSDP to achieve 2D parallelism. Whether using tensor parallelism alone or with FSDP, minimal changes to the training script are required.

